Level 2 process

Source: vignettes/level_2.Rmd

Samples standardisation

The second level of the t3 process aim to standardize samples data. These standardization was divided into 8 steps:

Process Code/method associated Class(es) associated
Process 2.1: sample length class ld1 to lf conversion sample_length_class_ld1_to_lf() full_trips
Process 2.2: sample number measured extrapolation sample_number_measured_extrapolation() full_trips
Process 2.3: sample step length class standardisation sample_length_class_step_standardisation() full_trips
Process 2.4: well set weight categories well_set_weigth_categories() full_trips
Process 2.5: standardised sample creation standardised_sample_creation() full_trips
Process 2.6: sample number standardisation standardised_sample_set_creation() full_trips
Process 2.7: raised factors determination raised_factors_determination() full_trips
Process 2.8: samples number standardisation at set scale raised_standardised_sample_set() full_trips

Process 2.1: sample length class LD1 to LF conversion

During the sampling process, fishes length can be collected and expressed in different standards. For example, regarding field constraints and more precisely the length of the different species, sampling data covered in T3 can by express in first dorsal length (LD1) or curved fork length (LF). Generally, length of small individuals are provided in LF because it’s logistically possible and easier to measure the entire fish, while length of bigger individuals are provided in LD1, for the same reciprocal reasons.

This step aim to standardise this standard among sampling data and at the end have only lenght sampling data expressed in LF. Historrical and so far, the process use a referential conversion table LD1 to LF. This table are expressed and used throught a stratification by ocean and specie. You can find an example of a part of it in the table 1 below.

Ocean Specie LD1 length class LF length class Distribution ratio
Atlantic YFT 38,0 132 4
Atlantic YFT 38,0 134 7
Atlantic YFT 38,0 136 16
Atlantic YFT 38,0 138 23
Atlantic YFT 38,0 140 23
Atlantic YFT 38,0 142 16
Atlantic YFT 38,0 144 7
Atlantic YFT 38,0 146 4
Table 1: Conversion LD1 to LF referential table for the YFT (Thunnus albacares) in the Atlantic Ocean.

Like you can see in the table 1, for one LD1 length class we have several LF length classes. That mean that in our data processed the number of sampling item could rise. Furthermore, tunas regional fisheries management organisations, like International Commission for the Conservation of Atlantic Tunas (ICCAT) or the Indian Ocean Tuna Commission (IOTC), have validated conversion factors for types of size measurements. One of our next update will be to modify the process according theses formula.

The global process flowchart is available in the figure 1 below.

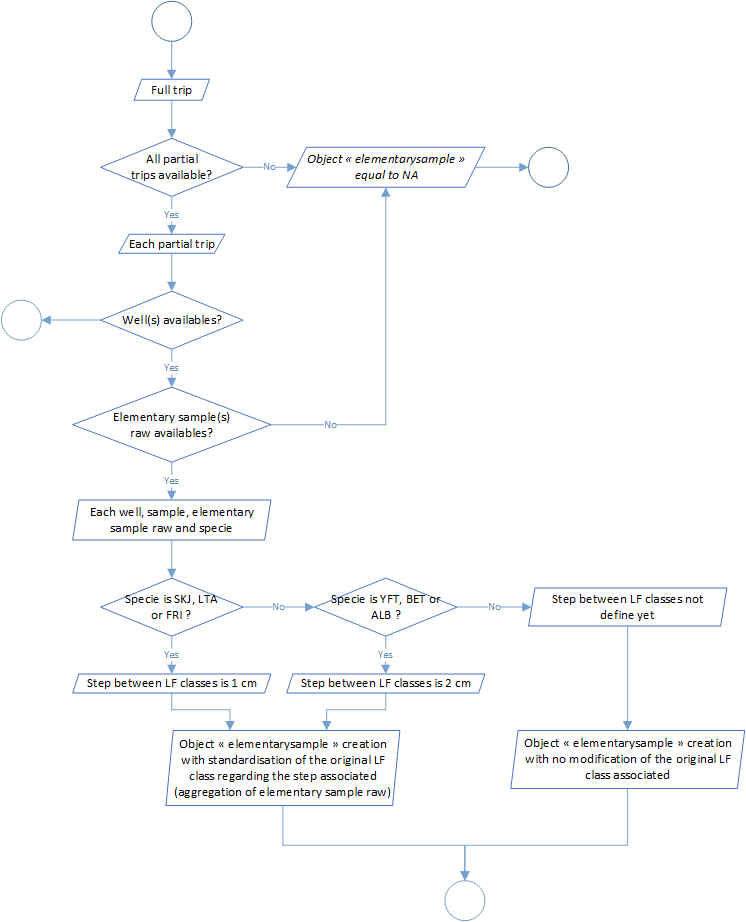
Figure 1: Sample length class LD1 to LF conversion flowchart.

Process 2.2: sample number measured extrapolation

During the sampling and according to the protocole, just a part of the sampled individuals are measured in comparision of the one counted. This step aim extrapolate sample number measured individuals to sample number individuals counted.

A Raising Factor (RF4) is calculated stratified by well, sample, sub-sample and specie. He is equal by strate to the sum of each counted individuals divided by the sum of measured individuals (after conversion of measure in curved fork length in the process 2.1).

The global process flowchart is available in the figure 2 below.

Figure 2: Sample number measured extrapolation flowchart.

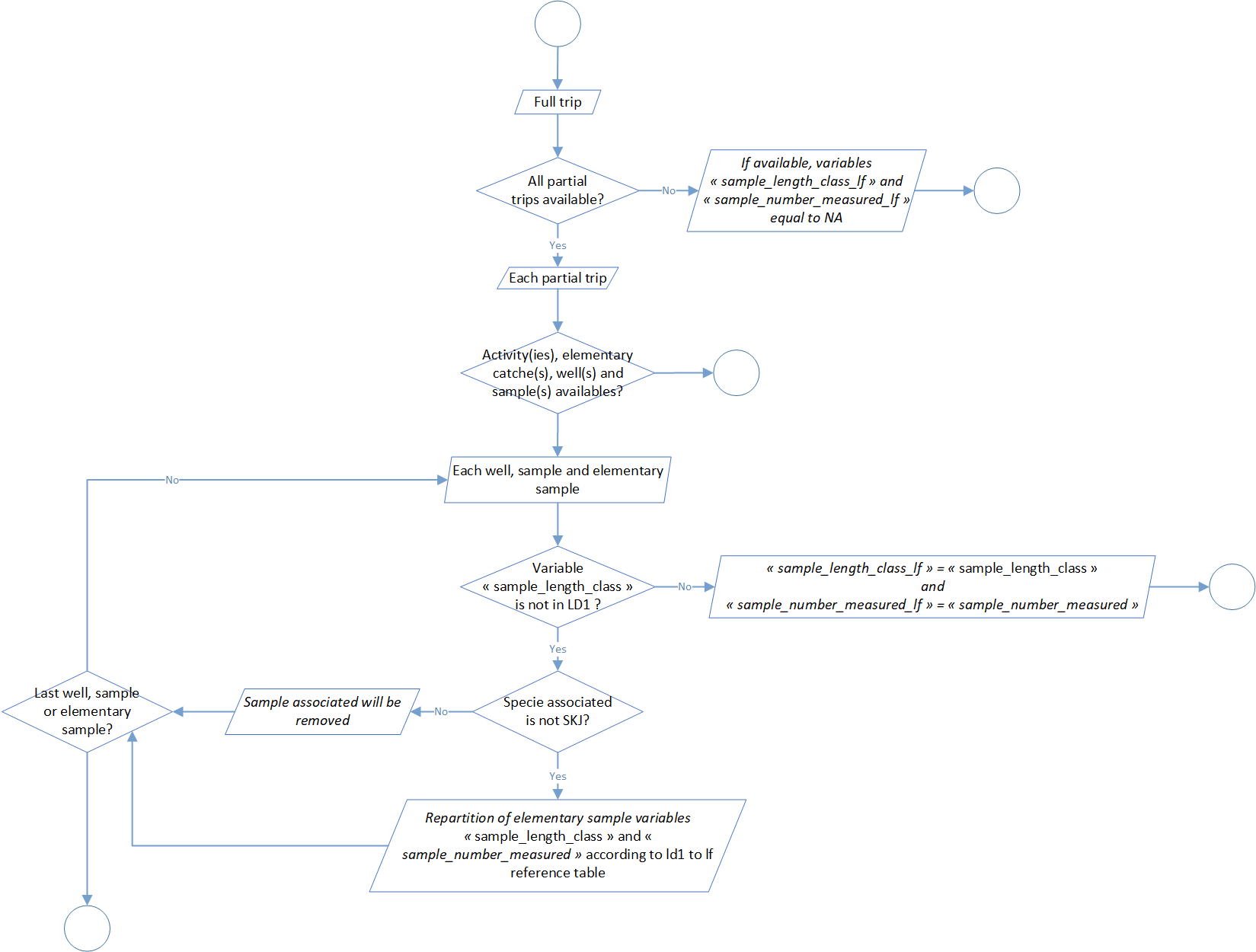
Process 2.3: sample step length class standardisation

LF length classes used during the treatment are not necessary the same that filled during the sampling. Furthermore, even if the actual sampling protocol detail what kind of lenght classes we have to use by specie, it’s not impossible to have differencies regarding this length classes if we mix “old data” with the actual one. In addition, it’s possible that the protocol could evolve in the future.

According to that, this step aim to standardise sample length classes. So far, these specifications are integrate in the process:

  • a length classes step of 1cm for SKJ (Katsuwonus pelamis), LTA (Euthynnus alletteratus) and FRI (Auxis thazard),
  • a length classes step of 2cm for YFT (Thunnus albacares), BET (Thunnus obesus) and ALB (Thunnus alalunga).

The global process flowchart is available in the figure 3 below.

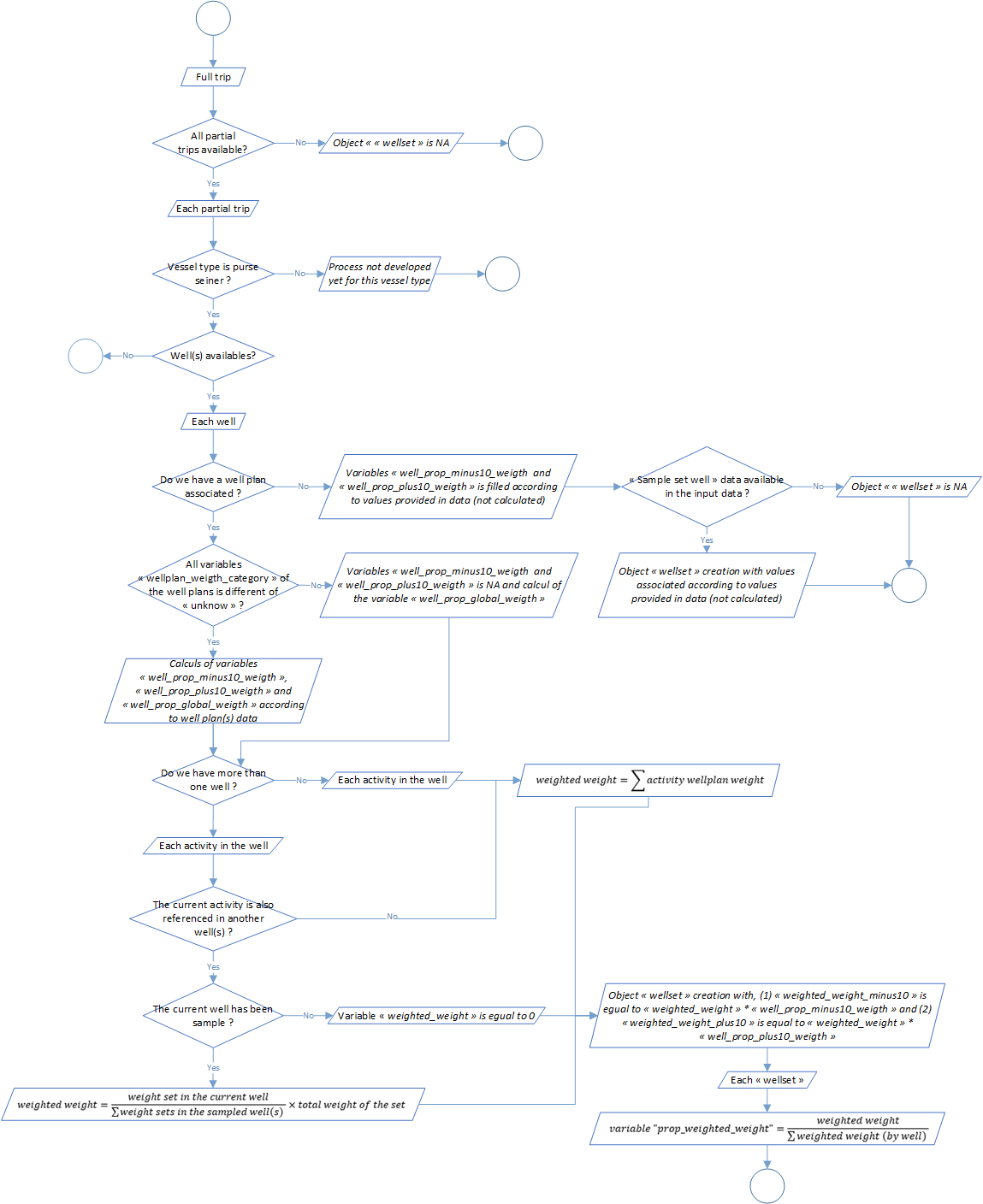
Figure 3: Sample step length class standardisation flowchart.

Process 2.4: well set weight categories

The sampling provides information at the well scale. However, a set could be displayed between several wells and sampled individuals could belong to as much as sets in the well.

This process aim to calcul a weighted weigth, which represent the weight of a set in a well, regarding the repartition of this set in all the wells. The global formula is the following one:

WW=W1W2×WTWW = \displaystyle \frac{W1}{W2} \times WT

Where WW is the Weighted weight, W1 is the weight of the set in the well, W2 is the weight of the set in all the sampled wells and WT the total set weight.

So far, the process is developed for the purse seiner. To better understand what the process do, take a look to an example. A set of 90 tonnes is display in 3 wells, 40 tonnes in the first one, 30 tonnes in the second and 20 tonnes in the last one. The wells 2 and 3 were sampled but no the first one. For the second well, the weighted weight will be equal to 54 tonnes (30 / 50 x 90). For the third one, the weighted weight will be equal to 36 tonnes (20 / 50 x 90).

Furthermore, a proportion of each samplings sets among the sampling well will be calculated in relation with the weighted weight:

PWW=WWi,j∑i=1nWWi,j PWW = \displaystyle \frac{WW_{i,j}}{\sum_{i=1}^{n} WW_{i,j}}

Where PWW is the proportionnal weighted weight and WWi,j is weighted weight of the current set i in well j.

The global process flowchart is available in the figure 4 below.

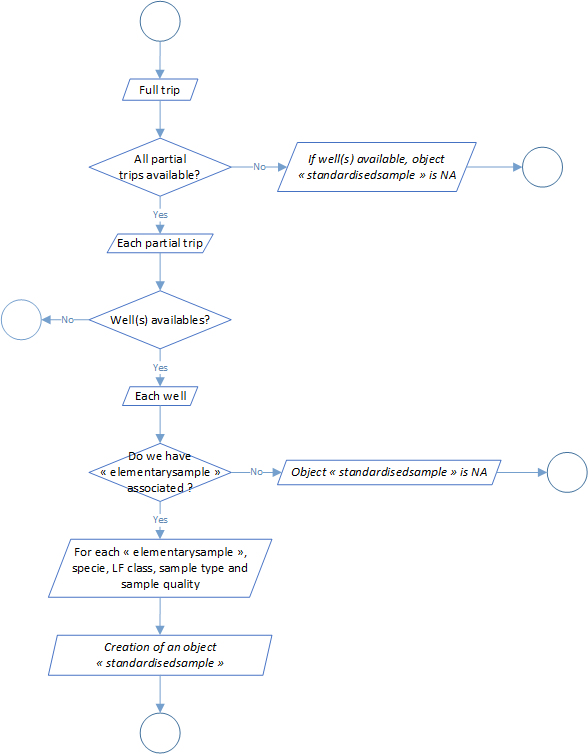
Figure 4: Well set weight categories flowchart.

Process 2.5: standardised sample creation

This process aims to sum up the samples according to the update made from the processes 2.1 to 2.3 on sample data. In this step we left behind all the notions of subsamples and we take into account the new-sample creation in the step above (for example when we make the conversion to LD1 to LF) and create a new object called standardised sample expressed at the scale of the trip, the well, the sample (id, quality and type) and the specie.

The global process flowchart is available in the figure 5 below.

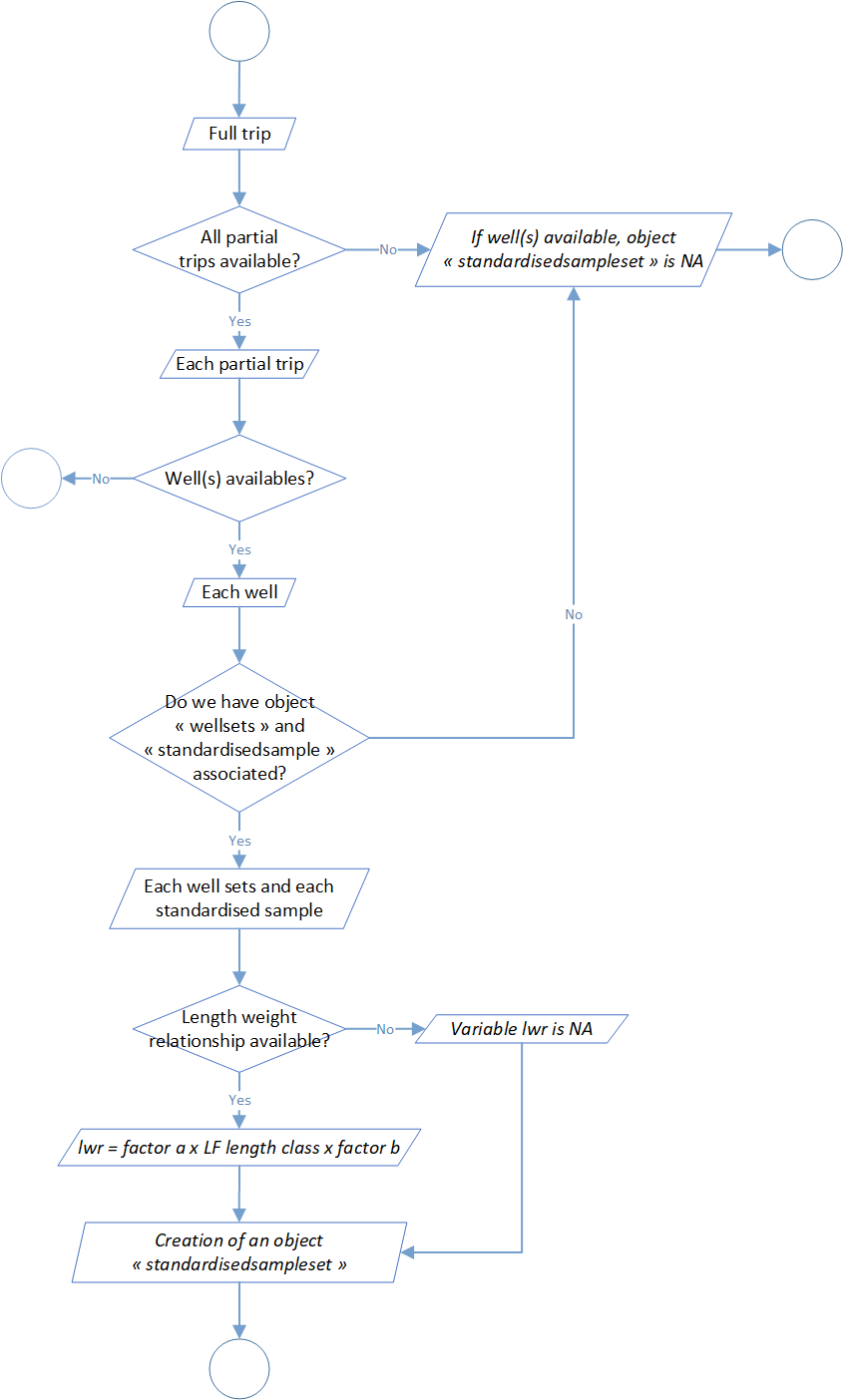
Figure 5: Standardised sample creation flowchart.

Process 2.6: sample number standardisation

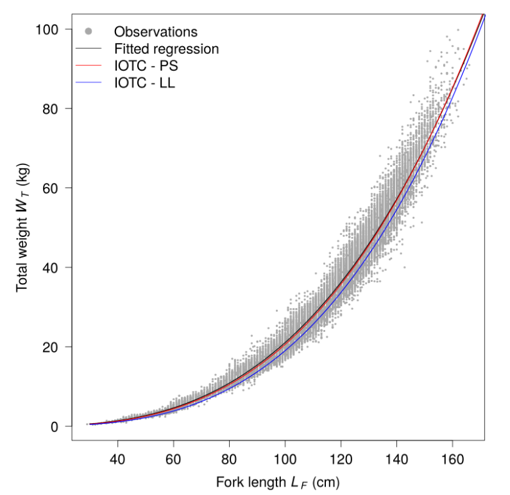
In the previous process and in the object standarised sample associated, samples is expressed at the well scale. In this step, the aim is to move to the expression of sample by well to sample by set. In the process 2.4, a weighted weight has been calculated and in addition a proportion of this weighted weight at the set scale. By combination of this value and elements of the object standarised sample, a new object called standardised sample set was created. Like explain before, this object is the expression of the sample at the set scale. Furthermore, this process made a conversion of the samples lenght measurements in weight by length weight relationship. Formula associated are the following one:

RWT=a×LFb RWT = a \times LF^{b}

Where RWT is the round weight, LF is the curved fork length and parameters a and b comes from a references table and are dependant of of the species and potentially of the area (ocean or others) and the season. More detail information could be find on the regional fisheries management organisations (RFMOs) like ICCAT (https://www.iccat.int/) or IOTC (https://iotc.org/).

In addition, you will find below in the table 2 the reference table for the length weight relationship and global process flowchart in the figure 6.

Ocean Specie code Specie name a b
Atlantic YFT Thunnus albacares 0,000021527 2,976000000
Atlantic SKJ Katsuwonus pelamis 0,000007480 3,252600000
Atlantic BET Thunnus obesus 0,000023960 2,977400000
Atlantic ALB Thunnus alalunga 0,000013718 3,097300000
Atlantic LTA Euthynnus alletteratus 0,000013770 3,035000000
Atlantic FRI Auxis thazard 0,000000280 4,135140000
Atlantic SKH Selachimorpha (Pleurotremata) 50,000000000 0,000000000
Atlantic BLF Thunnus atlanticus 0,000015400 3,080000000
Atlantic BON Sarda sarda 0,500000000 0,000000000
Atlantic BLT Auxis rochei 0,000007600 3,249000000
Atlantic FRZ Auxis spp, 0,000000280 4,135140000
Atlantic WAH Acanthocybium solandri 0,000003200 3,201000000
Atlantic MAW Scomberomorus tritor 0,500000000 0,000000000
Atlantic KGX Scomberomorus spp, 0,500000000 0,000000000
Atlantic SAI Istiophorus albicans 0,000004400 3,000000000
Atlantic BLM Makaira indica 0,000006500 2,960000000
Atlantic BUM Makaira nigricans 0,000003500 3,158000000
Atlantic WHM Tetrapturus albidus 0,000004600 3,000000000
Atlantic SPF Tetrapurus pfluegeri & T, belone 0,000004400 3,000000000
Atlantic BIL Istiophoridae spp, 0,000004400 3,000000000
Atlantic SWO Xiphias gladius 0,000007800 3,210000000
Indian YFT Thunnus albacares 0,000015849 3,046000000
Indian SKJ Katsuwonus pelamis 0,000005320 3,349580000
Indian BET Thunnus obesus 0,000027000 2,951000000
Indian ALB Thunnus alalunga 0,000006303 3,282500000
Indian LTA Euthynnus alletteratus 0,000013770 3,035000000
Indian FRI Auxis thazard 0,000000280 4,135140000
Indian SKH Selachimorpha (Pleurotremata) 50,000000000 0,000000000
Indian KAW Euthynnus affinis 0,000030000 2,908000000
Indian LOT Thunnus tonggol 0,000014300 3,000000000
Indian BLT Auxis rochei 0,000007600 3,249000000
Indian FRZ Auxis spp, 0,000000280 4,135140000
Indian WAH Acanthocybium solandri 0,000003200 3,201000000
Indian SFA Istiophorus platypterus 0,000016100 2,720000000
Indian BUM Makaira nigricans 0,000003500 3,158000000
Indian MLS Tetrapturus audax 0,000016500 3,062000000
Indian BIL Istiophoridae spp, 0,000004400 3,000000000
Indian SWO Xiphias gladius 0,000007800 3,210000000
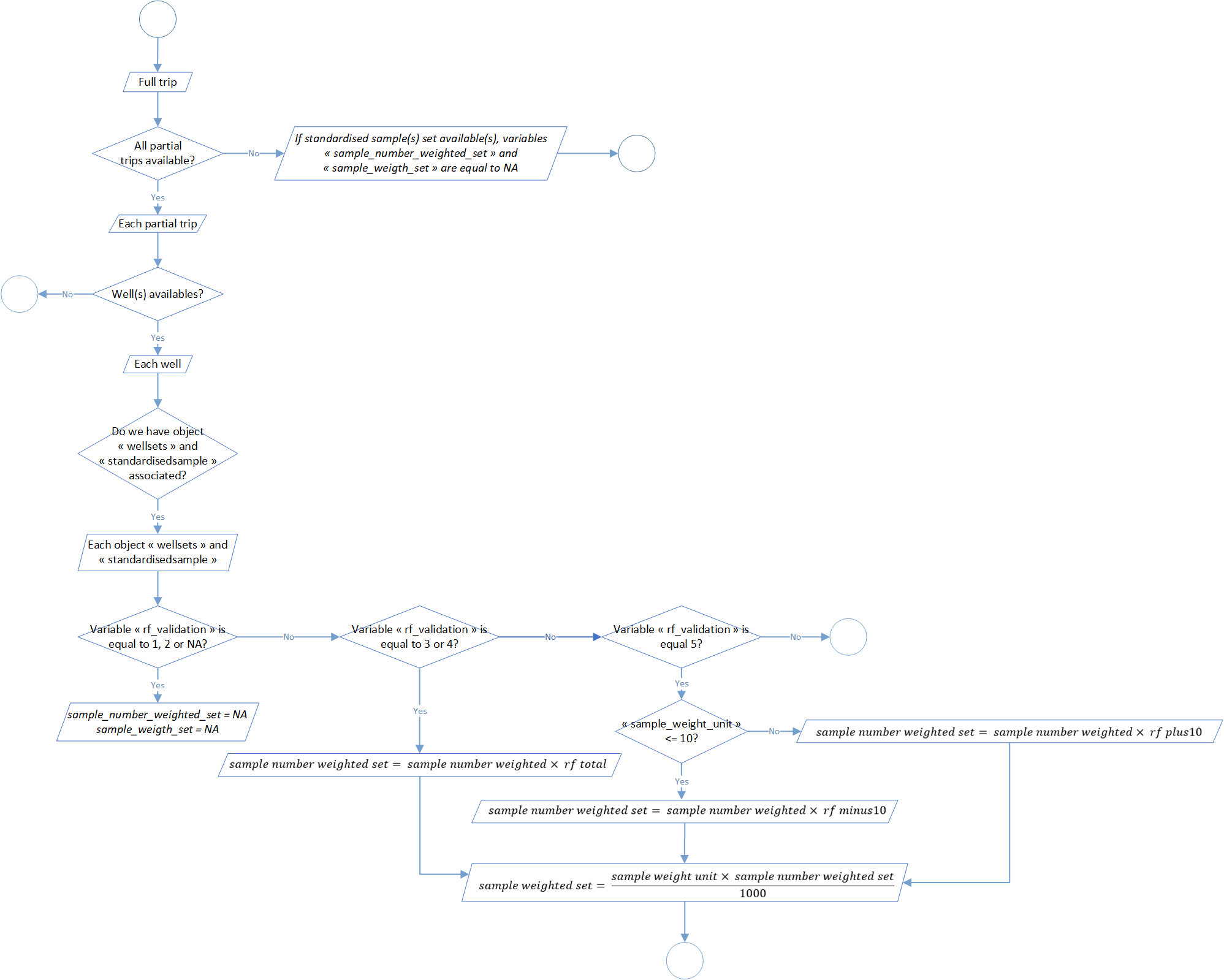
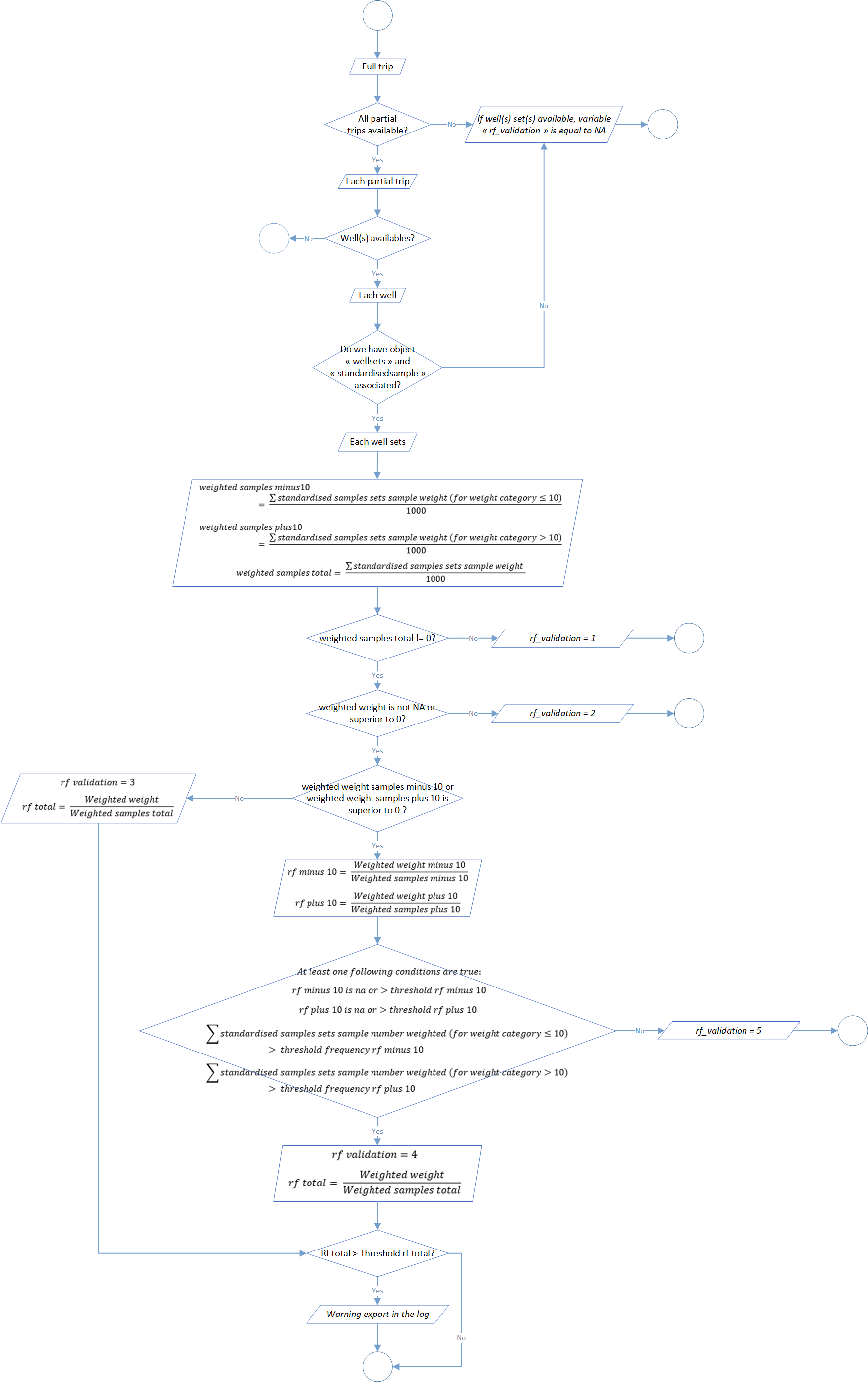
Table 2: Length weight relationship reference table.

Figure 6: Sample number standardisation flowchart.

Process 2.7: raised factors determination

The step aim to check relevance of the object standardised sample set by calculation of 6 parameters at the scale of each well sets: the number and the weight of sampled individuals, the total value and display by weight categories (<= 10kg or > 10kg).

5 diffetents scenarios are explain in the global flowchart of this process (figure 7). If it’s possible regarding data available, three raising factors are calculated related to the weighted weight of the set and sample weight (total and display by weight categories <= 10kg and > 10kg).

Verification thresholds could be modify in the function parameters through the arguments threshold_rf_minus10 (by default at 500), threshold_rf_plus10 (by default at 500), threshold_frequency_rf_minus10 (by default at 75), threshold_frequency_rf_plus10 (by default at 75) and threshold_rf_total (by default at 250).

Figure 7: Raised factors determination flowchart.

Process 2.8: samples number standardisation at set scale

This last step aim to express number and weight of sampled individuals at the scale of the set. The process use the factors calculated in the process 2.7.

The global process flowchart is available in the figure 8 below.

Figure 8: Samples number standardisation at set scale flowchart.